|
|
 |
| |
|
Sul
Terzo Giorno - Seconda Parte |
|
a cura di
Gaetano Barbella |
| |
|

|
|
IL TEMPO SECONDO
LA MITOLOGIA
|
|
|
|
LE ORE
|
|
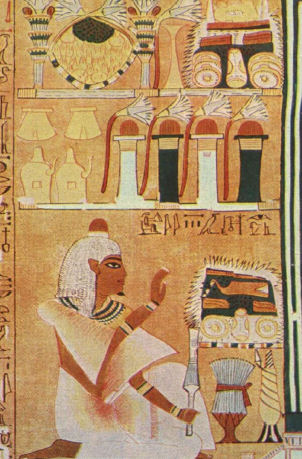 Le
Ore erano ritenute dai greci figlie di Giove e di Temi.
Presiedevano al corso delle stagioni; facendo nascere a suo tempo
fiori e maturare i frutti. Le Ore in principio erano tre:
Eunomia, Dice e Irene; ma più tardi diventarono quattro,
come le stagioni dell’anno. Esse stavano alle porte del Cielo con
Giano, e levavano le briglie ai cavalli del Sole. Filostrate le
descrive nel modo seguente: Le
Ore erano ritenute dai greci figlie di Giove e di Temi.
Presiedevano al corso delle stagioni; facendo nascere a suo tempo
fiori e maturare i frutti. Le Ore in principio erano tre:
Eunomia, Dice e Irene; ma più tardi diventarono quattro,
come le stagioni dell’anno. Esse stavano alle porte del Cielo con
Giano, e levavano le briglie ai cavalli del Sole. Filostrate le
descrive nel modo seguente:
«Le Ore scese
in terra vanno rivolgendo l’Anno, il quale è in forma di certa
cosa rotonda con le mani, dal quale rivolgimento viene che la terra
produce poi di anno in anno tutto quello che nasce e sono bionde
vestite di veli sottilissimi, e camminano sopra le aride spighe
tanto leggermente, che non ne rompono o toccano pur una. Sono di
aspetto soave giocondo, cantano dolcissimamente, e nel rivolger
quell’orbe, palla a circolo che sia, pare che porgano mirabile
diletto ai riguardanti; e vanno come saltando quasi sempre, levando
spesso in alto le belle braccia. Hanno i biondi crini alle spalle,
le guancie colorite, come chi dal corso si sente riscaldato, e occhi
lucenti, e al muoversi presti. A seconda delle stagione che le Ore
rappresentano, si coronavano d ghirlande, l’una di fiori, l’altra
di spighe, la terza di uva e pampani, l’ultima di olivo».
|
|
LE PARCHE
|
|
Le parche, secondo gli antichi greci, erano le Dee che presiedono alla sorte degli uomini, regolandone i destini. Sono sorelle e si
chiamano Cloto Lachesi e Atropo. Gli uni le fanno figlie della Notte e
dell'Erebo; altri della Necessità e del Destino, altri ancora di
Giove e di Temi. I greci le chiamavano Moire, e i Latini Parcae, dalla parola
parcus come se fossero state troppo avare nel dispensare la vita uomini che sembra troppo corta. Il loro nome particolare denota le loro differenti funzioni; perchè siccome ogni
destino degli uomini, che dicevasi sottomesso alla potenza delle Parche, riguardava o il tempo della nascita, o quello della vita o
quello della morte.
Cloto (che in greco significa evocazione) la più giovane delle sorelle, presiedeva alla nascita degli uomini, e teneva la
rocca e tirava il filo; Lachesi (che vuoi dire sorte) maggiore della precedente, avvolgeva il filo intorno al fuso, e Atropo (che significa senza ordine)
tagliava il filo con le forbici.
Lachesi nell’empire il fuso segna quel che accade nella vita di un uomo, in cui gli uni agli altri si succedono i giorni e le azioni, i
dolori, i piaceri, le vicende, le speranze, le illusioni, i disinganni. A ogni ora che passa s’incalzano le idee; i moti dell’animo, gli
avvenimenti; non si perde nulla tanto nella natura quanto nella morale: l’affaticarsi e l’avvicendarsi delle cose ha una regola e un fine
stabilito dall’ordine generale: e il fuso è un simbolo di quella successione delle cose umane che ha luogo nella vita, perchè conserva
il filo, non lo disperde, e sembra che lo destini, come negli usi volgari delle filatrici, a ordire qualche trama; e di fatti ogni vita d’uomo
concorre a formare il tessuto della società generale. Per cui Lachesi, benchè sia di minore attività delle altre due sorelle, ha un
incarico grave e misterioso.
Le Parche assistevano ai parti per rendersi padrone del bambino che nasceva. Secondo Esiodo sono le padrone assolute di tutto il
bene e di tutto il male che avviene nel mondo. Altri mitologi sottomettono le
Parche agli ordini di Plutone; ma l’opinione la più
generale è che le Parche servono sotto gli ordini del Destino, a cui gli Dei, e lo stesso Giove sono sottomessi. Platone, che le vuole
figlie della Necessità, rappresenta queste Dee sedute accanto alla madre alla quale pone fra le ginocchia un gran fuso di diamante
— egualmente distante l’una dall’altra; in alto ed elevato seggio; che cantano insieme con le Sirene, che sono sopra le sfere celesti.
Lachesi canta le cose passate; Cloto quelle presenti; Atropo, quelle dell’avvenire; e mettono parimenti mano al fuso insieme con la
Necessità loro madre in questo modo: Cloto vi mette la destra,
Atropo la sinistra, e Lachesi con ambo le mani lo tocca di qua e di là.
Comunemente queste Dee rappresentavansi con tre donne oppresse dalla vecchiezza, con in testa una
corona di lana e narcisi intrecciati, annodata da nastri bianchi e una veste parimenti bianca che copre loro tutto il corpo. La decrepitezza di queste Dee
denotava, secondo i moralisti, l’eternità dei decreti divini; la rocca e il fuso significavano che spettava a loro di regolare il corso della
vita, e il filo misterioso indicava il poco fondamento che si poteva fare di una vita che dipendeva da così poca cosa. La corona che
portavano in testa era segno del loro potere su tutto l’universo. Le
Parche adoperavano lana bianca, grigia e nera; la prima, per filare
giorni lunghi e felici; l’ultima, la vita corta e infelice. Si sacrificavano loro pecore nere, quantunque fossero state Dee implacabili. —
Non si trovano che pochissime figure delle Parche. |
|
LO SPIRITO DI
OSIRIDE (DEMETRA O CERERE): GRANO STORIA DI UN MITO
|
|
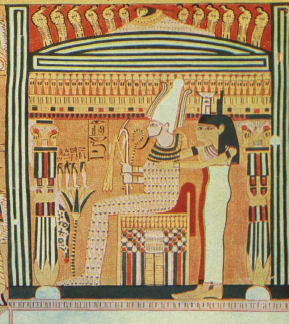
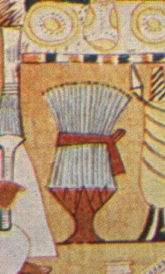 Il mito del grano legato allo «spirito del grano» del culto di Osiride ed in
seguito Demetra e Cerere greco-latine, nell'iconografia del papiro di
Ani, però, non trova buona corrispondenza se osserviamo bene
l'illustr.2. Non è il mazzo di grano che si vede, bensì - e chiaramente -
un plico di fogli di carta (ovviamente di papiri). Ma va bene lo stesso la Il mito del grano legato allo «spirito del grano» del culto di Osiride ed in
seguito Demetra e Cerere greco-latine, nell'iconografia del papiro di
Ani, però, non trova buona corrispondenza se osserviamo bene
l'illustr.2. Non è il mazzo di grano che si vede, bensì - e chiaramente -
un plico di fogli di carta (ovviamente di papiri). Ma va bene lo stesso la
metafora del grano legata allo «spirito di Osiride», poichè dice il
salmodiante «non di solo pane si vive, ma anche della parola del
Signore» che ci viene trasmessa con uno scritto (sul papiro con
inchiostro di bacche dagli antichi egizi). Ecco che il passo è breve per
intravedere, nel plico sotto il carro del sole dell'illustr.2, una certa
struttura di memoria come quella dei calcolatori (illustr.3). Da qui la
concezione di un campo di forze, del tutto simile a quello di un'elettrocalamita, che tiene sospeso il carro solare della vita. E qui
entrano in campo le Parche per dare il via alle Ore del flusso della vita
con un periodico oscillare del carro sovrastante: Ore, di un calice dolce
e/o amaro, quello nelle mani di Ani genuflesso. E' così meravigliosa
l'iconografia espressa dallo scriba Ani nel dipingere questi dettagli da
vederli aderire finanche alla meccanica di un orologio moderno come farò vedere fra poco. Per il resto sulla macchina del tempo lascio per ora parlare le illustrazioni e relative
didascalie.
|
| |
|
|
 |
|
 |
|
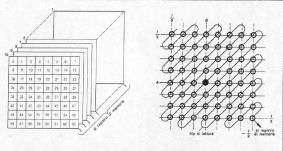
Illustrazione 3 – Struttura di una memoria a nuclei magnetici (a sinistra) e schema di un piano di memoria (a destra). Per il calcolatore ipotetico cui è riferita la discussione, si è assunta una memoria semplificata, a 10 piani (tanti quanti sono i bit per parola) e 64 bit per piano. Il secondo schema mette in evidenza, per ogni piano, la posizione dei nuclei, i fili di attivazione e il cosiddetto filo di senso o di lettura. (Tratto dalla «Enciclopedia della Scienza e della Tecnica», vol. II – Ediz. Mondadori) |
|
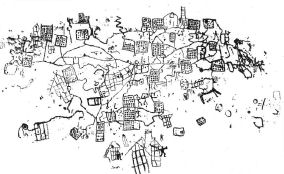
Illustrazione 4 - Incisioni rupestri della Valcamonica (BS). Il parco di naquame a Capo di Ponte. Sulla base di una radice geometrica insita nel pensiero degli antichi egizi (Vedasi testo dell'autore "Alla radice dell'intelligenza matematica"), I "quadrati" di Naquame potrebbero essere interpretati come una struttura di memoria analoga a quella dei calcolatori (illustr. 3). (Tratto da «Capo di Ponte e le incisioni rupestri », ediz. Guide Grafo di Brescia) |
| |
|
|
 |
|
 |
|
Illustrazione 5 - Dettaglio illustr. Di copertina. Il corpo di Osiride in trono è come un ideale magnete. Nell'insieme ogni cosa è informata al suo orientamento. In alto all'esterno i 12 serpenti (i mesi dell'anno) rappresenterebbero le linee di forza magnetiche come quelle della Terra concepita come una geodinamo (illustr.7a) |
|
Illustrazione 6 - Rappresentazione didattica di magneti elementari in un asta di ferro raffigurati come aghi di bussola. A destra è il caso di un asta amagnetica; a destra l'asta è magnetica come il corpo di Osiride (illustr.5). (Tratto da «Corso di Elettronica», Istituto Svizzero di Tecnica di Luino) |
| |
|
|
 |
|
 |
|
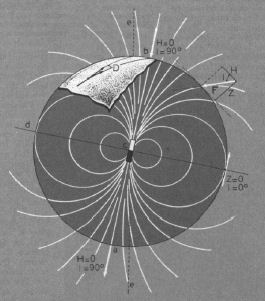
Illustrazione 7b - Statua-menhir Ossimo 9. Si noti la somiglianza del disco solare con le linee magnetiche terrestri dell'illustr. 7a. (Tratto da «Capo di Ponte e le incisioni rupestri », ediz. Guide Grafo di Brescia) |
|
Illustrazione 7a - La Terra ipotizzata come geodinamo. (Tratto dalla «Enciclopedia della Scienza e della Tecnica», ediz. Mondadori. |
|
|
|
|
|
LA SCATOLA DEL TEMPO DI ANI E LA CONCEZIONE DELL'OROLOGIO
RICHIAMI SPECIFICI SULL'OROLOGIO MECCANICO CONVENZIONALE
www.orologeria.com/italiano/rivista/rivista6.htm
|
|
|
|
DALLA MOLLA AL
BILANCIERE
|
|
Tutti sanno per linee generali come funziona un orologio. Perciò proviamo ora ad entrare nei dettagli e a capire in che modo
l'energia, che passa dalla molla al bilanciere, possa essere trasformata in un misuratore di secondi. Iniziamo con l'analizzare il
gruppo bilanciere-spirale. Immaginiamo un bilanciere che possa muoversi liberamente, avendo fissata l'estremità della spirale al
ponte (è sufficiente levare l'àncora) e diamo una piccola spinta al suo volantino. La prima cosa che noteremo sarà che, grazie alla
spirale ed al suo espandersi e contrarsi, si muoverà avanti e indietro con ampiezze sempre minori fino a fermarsi del tutto: definiamo
subito questo movimento. Se fossimo in mancanza di attriti, avremmo risolto subito il primo dei nostri problemi, perché il bilanciere
continuerebbe a marciare all'infinito. Ma nella realtà queste oscillazioni diminuiranno progressivamente di ampiezza per arrestarsi
poi del tutto. Quello che ci interessa però è vedere che le oscillazioni saranno sempre della medesima durata, pur diminuendo di
ampiezza. Questo perchè diminuisce la distanza percorsa, ma diminuisce anche la velocità del punto P. Ci troviamo di fronte ad un
fenomeno periodico ed isocrono. Noi dobbiamo fare in modo che questo movimento resti costante nel tempo, e non si esaurisca
dopo poche oscillazioni. Per fare questo dobbiamo rinnovare periodicamente la spinta che abbiamo dato all'inizio. Questo è possibile
dando dei piccoli impulsi al bilanciere attraverso l'àncora, che a sua volta riceve l'impulso dalla ruota di
scappamento. Ora però dobbiamo fare in modo che queste alternanze si possano contare e riportare in maniera leggibile: entra in gioco quindi il treno di ruote che dalla molla trasmette il moto al bilanciere.
|
|
|
|
 |
 |
 |
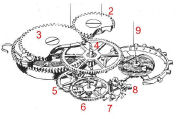
| Illustrazione 8
– Bilanciere |
Illustrazione 9
– Gruppo di scappamento |
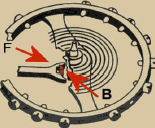
Illustrazione 10 – Rocchetto
bottone del disco |
 |
 |
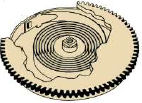 |
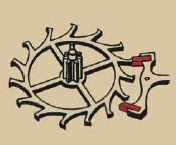
| Illustrazione 11 – Leve d'àncora |
Illustrazione 12 – Ruota centro |
Illustrazione 14 –
Bariletto |
|
 |
|
|
Illustrazione
13 – Molla svolta |
|
|
|
|
|
|
Rif. Illustr.8 - Definiamo “oscillazione” il percorso che fa un punto P nel volantino del
bilanciere partendo da A per arrivare a B e tornare ad A. La metà esatta di questo
viaggio, e cioè il percorso A-B (o il ritorno B-A) è detta “alternanza”.
Abbiamo così chiarito cosa significa avere un orologio che fa 18.000 alternanze/ora:
vuol dire che compie per 9000 volte il percorso A-B e per altre 9000 il ritorno B-A
Rif. Illustr. 10 - L'àncora agisce sul bilanciere con la sua parte terminale chiamata
“forchetta” (F) che lavora sul bottone del disco (B) del bilanciere.
Rif. Illustr. 9, 10 e 11 - Dall'altra parte l'àncora ha due leve che, ricevendo l'impulso
dalla ruota di scappamento, trasformano il moto rotatorio della ruota stessa in moto
alternativo del bilanciere.
Rif. Illustr.12 - Per rendere semplice il discorso, dobbiamo fare riferimento alla ruota centro, che possiamo individuare nell'illustr.12.
E' infatti sul perno della ruota centro che viene innestata la lancetta dei minuti e da questo prende il moto anche la lancetta delle ore.
Nel caso del nostro orologio dobbiamo fare in modo che alle 18.000 alternanze/ora del bilanciere corrisponda un giro completo della
ruota centro e di conseguenza della lancetta dei minuti. Vediamo prima come è fatta una ruota di un orologio. Sopra, dall'illustr.12
possiamo vedere che essa di solito è composta da una ruota dentata vera e propria, generalmente in ottone, fissata ad un asse in
acciaio chiamato pignone, anch'esso dentato (i denti del pignone tradizionalmente vengono chiamati ali). Come si può notare nel
disegno, ogni ruota ingrana col pignone della ruota successiva, fino ad arrivare alla ruota di scappamento che lavora con l'àncora.
Rif. Illustr.13 e 14 - Arriviamo ora alla fonte di tutta l'energia che il bilanciere ed il treno degli ingranaggi si incaricano di
trasformare in un dato leggibile: la molla. La molla è una striscia di acciaio che viene avvolta su sé stessa ed inserita in un contenitore metallico chiamato
bariletto. La molla libera deve avere approssimativamente la forma di una S, quando vediamo molle che fuori del bariletto hanno quasi tutte le
spire avvolte su sè stesse, siamo di fronte ad una molla esausta e che deve essere sostituita. La funzione del bariletto è
molteplice. La molla viene inserita nel bariletto perché è più riparata dagli agenti atmosferici. La polvere che potrebbe depositarsi tra
le spire della molla contribuisce ad aumentare di molto gli attriti e di conseguenza l'energia rilasciata dalla molla è minore e meno
costante. Inoltre, senza questa polvere, il lubrificante messo per la molla resta più a lungo in posizione e in buone condizioni. In caso
di rottura della molla - rottura che spesso avviene nella fase di massima carica della stessa - le ruote e gli ingranaggi del movimento
sono al riparo della molla “impazzita”. Anche se bisogna dire che questo problema si presenta comunque perché l'energia rilasciata
alla molla durante la rottura si scarica sul bariletto e sulla prima ruota a contatto con esso, causandone la rottura. I danni in questo
caso sono però limitati ai denti del bariletto e della ruota. La molla è fissata alla parete del bariletto con un gancio, come si vede
nell'illustr 14. Nel corso degli anni gli attacchi delle molle hanno avuto delle evoluzioni. Si è passati dal foro vero e proprio sulla molla
che si fissava ad un gancio sul bariletto, agli attacchi moderni, costituiti da una piccola brida saldata alla parte terminale della molla
e che va a bloccarsi in un intaglio praticato sulla parete del bariletto. Negli orologi automatici, la brida è più lunga e non si aggancia
al bariletto: serve per far slittare la molla, una volta raggiunta la massima carica, per non danneggiare il dispositivo di carica
automatica. In pratica finché la molla non è del tutto carica, la pressione delle spire esterne tiene la brida ferma contro la parete del
bariletto. Quando la molla si carica ulteriormente, questa pressione diminuisce, fino a far slittare la molla, scaricandola quanto basta
perchè le spire esterne tornino a premere sulla brida. Uno dei problemi che assillava i costruttori di orologi era la poca omogeneità
nell'erogazione dell'energia da parte della molla.
|
|
L'OROLOGIO
MECCANICO DI ANI
|
|

|
|
Illustrazione 17 – Dettaglio del papiro di Ani della pesatura del cuore. Il dio del
male Seth |
|
|
Può essere sembrato superflua, se non eccessiva, la spiegazione della
meccanica dell'orologio meccanico convenzionale, presa a prestito dal
sito di un rinomato costruttore d'orologi e oggetti d'oreficeria. Ma non
credo proprio perchè tutto questo tempo è servito per immaginare dove
e come identificare le tre Parche e lo spirito di Osiride in azione, del
supposto orologio di Ani, nell'orologio meccanico da poco rappresentato. Io credo che più di un lettore l'abbia capito per dire: che
Lachesi (quella che predispone il filo della vita) è il
bilanciere (illustr. 8 ); che Cloto e Atropo (l'inizio e fine della vita)
è nel gruppo di scappamento (illustr. 9, 10 e 11); infine che lo spirito di Osiride (forza
serpentina della vita, magnetismo) è nella molla collocata nel
bariletto (illustr.13 e 14). |
|
|
E le Ore o i secondi, scanditi dall'orologio
meccanico,riguardano il calice, dolce e/o amaro in mano ad Ani. Ci si domanda,
ora, come capire, dall'iconografia del papiro di Ani, la meccanica riguardo il dolce e/o l'amaro della vita?
Per ottenere i lumi in proposito occorre ricorrere alla relativa visione d'insieme. Innanzitutto si capirà che al
dolce corrisponde il biancore in genere, viceversa all'amaro la
nerezza. Lasciando al lettore la possibilità di intravederne le rispettive nature attraverso ciò che è rappresentato in
bianco ed in nero nei due quadri del
papiro di Ani, in particolare la scatola del sole, ossia la macchina del tempo (illustr.1), presenta il biancore
simile a fioritura all'esterno e la nerezza all'interno. Si rivela già una cosa stupefacente
all'interno, la rappresentazione di un volatile che sembra imbeccare il suo pulcino che si erge dal nido. Il tutto relativo dà
esattamente l'idea di un'ampolla a mercurio che si usa in elettrotecnica come interruttore inclinandolo di un
certo angolo. In posizione orizzontale (di riposo) i contatti sono aperti. Ossia non c'è passaggio di corrente,
ma non appena l'interruttore si inclina come previsto, e con esso il mercurio (che è come un liquido), si
stabilisce il contatto elettrico. Iconograficamente questo contatto riguarda il becco del volatile madre che nutre
il figlio: veramente ammirevole! Se le cose della vita, proiettate secondo la rappresentazione iconografica di
Ani, procedessero senza intoppi (cosa che sembra scontata grazie allo zelante scriba Ani), le Ore
trascorrerebbero tranquille e la notte si avvicenderebbe al giorno. Questo, però, a patto che gli equilibri fra il
bene (Ani genuflesso davanti al suo dio Osiride) ed il male (la bestia del dio Seth alle spalle di
Thoth, protettore della magia) del quadro della pesatura del cuore di Ani, siano perfettamente in pari. Si sarà notato
che entrambi sembrano che galleggino su vasche di liquidi diversi che sono però sullo stesso livello (diversi
ma corrispondenti trattandosi di due corpi che si compenetrano in quello di Ani). Ho già accennato, nel
descrivere le mie ipotesi sulle corrispondenze della legge fisica di
Ferrel, sulla natura del dio Seth che appare come un “pallore
gonfiato” (illustr.17). Dunque ipotizzando un calo di pressione
dell'otre-Seth, immaginandolo pieno di gas (perchè la pompa sotto la sua ascella non esprime la forza propulsiva sufficiente), avviene che
questi si affloscia immergendosi nel liquido sottostante. Ecco che per effetto idrostatico
dei “vasi comunicanti”, dalla parte di Ani genuflesso (illustr. 1), qualcosa cambia sotto di sé alterando inevitabilmente il suo assetto.
Simultaneamente cambia il delicato equilibrio del piano di appoggio delle «Parche» e del vaso dello «spirito di
Osiride», che vi corrisponderebbero, e avviene ciò che cambia in modo potente il corso degli eventi
segnati dalla nostra macchina del tempo in discussione. E qui, ora viene il bello del lato della ricerca che
continuamente si sta facendo sul conto degli antichi egizi. In verità si
tratta del “brutto” visto che il soggetto sotto osservazione è il dio del male Seth. Dunque ci siamo resi conto della necessità della funzione di
“pallone gonfiato” di Seth, e già questo ci porta a giustificarne il significato traslato al genere d'uomo che vi
corrisponde. In più riscontriamo dei dettagli che solo la fisica meccanica spicciola ne chiarisce la funzione
specifica perchè sia a tutti gli effetti come un serbatoio a pressione. Chi non sa che per comprimere un gas e
introdurlo in un serbatoio ha bisogno di un compressore? E' una funzione che si esplica grazie una sorta di
ruota a palette che gira velocemente del tutto simile ad un comune ventilatore, e a quella disegnata in
corrispondenza dell'ascella di Seth. Ci si chiede, poi, da dove e come proviene il presunto
“gas”? Secondo me dalla parte addominale rappresentata nel modo che si vede
chiaramente, ossia con una serie continua di virgolette come se fosse una comune griglia
d'areazione. Ma qui, ora si presenta un altro caso, la cui possibile mia interpretazione mi fa sobbalzare sorpreso. Secondo le regole dell'aerodinamica il fluido, che
attraversa questo tipo di griglia, fuoriesce con regime di turbolenza. E questo, con un lampo di
genio, mi ha portato a dare rilievo alla teoria aerodinamica che spiegherebbe l'incredibile volo dei calabroni che con le ali
così piccole sfida le leggi di sostentamento. Non solo, ma il supposto regime di turbolenza spiega le tante
macchie nere diffuse nel corpo di Seth che rappresenterebbero gli elementi vorticosi capaci di sostentarsi. Su
questo tema così interessante, pieno di sorprendenti interrogativi, riporto di seguito un articolo scientifico
che spiega ogni cosa anzidetta, e che ho tratto dal sito
www.cicap.org/articoli/at101780.htm
(a sua volta rilevato da Scienza & Paranormale n. 53). Chi lo ha redatto è Andrea Albini, funzionario tecnico del Dip. di Ingegneria
Elettrica dell'Università di Pavia.
|
|
L'ENIGMA DEL
CALABRONE CHE NON POTEVA VOLARE
|
|
 Anche se la scienza e i suoi impieghi tecnologici sono ripetutamente promossi dai
media e ricevono un certo interesse di pubblico - soprattutto per i loro usi in campo
medico e biologico - mai come negli ultimi decenni questo settore ha avuto così seri
problemi di immagine. Dimenticando che anche in questo caso si tratta di attività
umane, e come tali soggette alle regole morali e sociali che la comunità decide di
applicare attraverso l’impegno individuale e collettivo, molti tra coloro che si sentono a
disagio con la scienza preferiscono rifugiarsi nella contrapposizione ideologica; oppure
nella fuga in un passato mai esistito in cui tutto era in armonia con la natura. Si
ripropone, in pratica, l’antica "reazione" romantica ottocentesca che vedeva nella
natura qualcosa di buono a priori, la cui imitazione non era solamente sacrilega ma
anche un grave errore di presunzione. Quest’atteggiamento a volte traspare nelle
conversazioni di tutti i giorni. Quante volte ci siamo sentiti rivolgere un'osservazione di
questo tipo: "Perché, se la scienza è veramente quello che vuol far credere di essere non è in grado di dare una spiegazione al
fatto che un insetto così pesante e con ali così piccole come il calabrone riesce,
nonostante tutto, a volare?" Nessuno scienziato con un minimo di esperienza pratica si
sognerebbe di predicare l’onnipotenza della sua disciplina, né di mettere
in discussione l’ingegnosità dei risultati di una lunghissima evoluzione biologica negli organismi; anche
perché, ovviamente, la contestazione è intesa principalmente come un elemento di riflessione morale. Personalmente, sono convinto che accuse di questo
tipo siano fondamentalmente sbagliate; come ho detto sopra, la riflessione non dovrebbe rivolgersi
verso la scienza "in sé" ma piuttosto verso chi la pratica, analizzando il suo grado di libertà, i condizionamenti che riceve e le sue possibilità di reagire e avere
voce in capitolo. Per quanto riguarda il calabrone, non resta che affrontare la questione
specifica: siamo proprio sicuri che gli scienziati non siano in grado di spiegare perché questo insetto è in grado di volare? Anche se la scienza e i suoi impieghi tecnologici sono ripetutamente promossi dai
media e ricevono un certo interesse di pubblico - soprattutto per i loro usi in campo
medico e biologico - mai come negli ultimi decenni questo settore ha avuto così seri
problemi di immagine. Dimenticando che anche in questo caso si tratta di attività
umane, e come tali soggette alle regole morali e sociali che la comunità decide di
applicare attraverso l’impegno individuale e collettivo, molti tra coloro che si sentono a
disagio con la scienza preferiscono rifugiarsi nella contrapposizione ideologica; oppure
nella fuga in un passato mai esistito in cui tutto era in armonia con la natura. Si
ripropone, in pratica, l’antica "reazione" romantica ottocentesca che vedeva nella
natura qualcosa di buono a priori, la cui imitazione non era solamente sacrilega ma
anche un grave errore di presunzione. Quest’atteggiamento a volte traspare nelle
conversazioni di tutti i giorni. Quante volte ci siamo sentiti rivolgere un'osservazione di
questo tipo: "Perché, se la scienza è veramente quello che vuol far credere di essere non è in grado di dare una spiegazione al
fatto che un insetto così pesante e con ali così piccole come il calabrone riesce,
nonostante tutto, a volare?" Nessuno scienziato con un minimo di esperienza pratica si
sognerebbe di predicare l’onnipotenza della sua disciplina, né di mettere
in discussione l’ingegnosità dei risultati di una lunghissima evoluzione biologica negli organismi; anche
perché, ovviamente, la contestazione è intesa principalmente come un elemento di riflessione morale. Personalmente, sono convinto che accuse di questo
tipo siano fondamentalmente sbagliate; come ho detto sopra, la riflessione non dovrebbe rivolgersi
verso la scienza "in sé" ma piuttosto verso chi la pratica, analizzando il suo grado di libertà, i condizionamenti che riceve e le sue possibilità di reagire e avere
voce in capitolo. Per quanto riguarda il calabrone, non resta che affrontare la questione
specifica: siamo proprio sicuri che gli scienziati non siano in grado di spiegare perché questo insetto è in grado di volare?
|
|
NASCE UN LEGGENDA
|
|
Secondo l’ingegnere aeronautico John McMastes, la storia del calabrone iniziò a circolare in Germania negli anni Trenta del secolo
scorso e precisamente all’università di Göttingen: proprio il luogo in cui Ludwig Prandtl (1875-1953) gettò le basi della moderna
fluidodinamica1. Secondo McMastes, il primo a proporre questo enigma fu un professore svizzero, da tempo scomparso, che
aveva svolto studi pionieristici sulla dinamica dei gas a velocità supersoniche nel corso degli anni Trenta e Quaranta. La storia vuole
che durante una cena questo scienziato ebbe una conversazione con un collega biologo il quale gli pose la domanda fatidica: "che
proprietà aerodinamiche avevano le ali dei calabroni per permettere loro di volare". Lo scienziato fece alcuni rapidi calcoli,
immaginando che le ali di questi insetti fossero lisce e prive di increspature. Le
conclusioni furono sorprendenti: in base ai calcoli, i calabroni non dovevano essere in grado di sostenersi nell’aria! Evidentemente qualcosa non tornava. Ben presto lo studioso tedesco
si accorse che l’errore risiedeva nella sua assunzione di partenza: come un esame al microscopio gli aveva confermato, le ali di
questi insetti non erano affatto lisce. Ormai era troppo tardi per arrestare il mito dell’impossibilità del volo del calabrone che aveva iniziato a propagarsi di bocca in bocca, anche grazie all’aiuto di giornalisti e divulgatori scientifici. Già nel 1957, J. Pringle, autore di
un classico studio sulla meccanica del volo degli insetti, era stato in grado di ricostruire alcuni dei momenti più significativi del
propagarsi della leggenda. Più che ricostruirne le fasi, è interessante esaminare le ragioni che portarono inizialmente a valutare
l’impossibilità del volo del calabrone e successivamente analizzare attraverso quali accorgimenti fisici questi insetti riescono
effettivamente a sostenersi nell’aria.
|
|
PERCHE' VOLANO I
CALABRONI
|
|
Le considerazioni iniziali dell’anonimo scienziato tedesco, presupponevano che se le ali dei calabroni avevano una superficie liscia,
dovevano avere un numero di Reynolds molto basso. Con questo termine, che prende il nome di un noto ingegnere meccanico
dell’Ottocento, siamo in grado di avere una valutazione del rapporto tra le forze di
viscosità di un fluido e quelle inerziali, ossia il prodotto della massa di un oggetto che si
muove attraverso di esso per l’accelerazione che subisce. Una particella di polvere che
galleggia nell’aria ha numeri di Reynolds molto bassi (da 1 a 10) mentre i jet a reazione hanno valori che superano i dieci milioni. Le
ali degli insetti si situano nella parte basse di un grafico che rappresenta la velocità rispetto ai numeri di Reynolds con valori tra 100
e 10.000. Un modo per rappresentarci questa situazione è quello di immaginare che essi
debbano volare con le loro piccole ali in un fluido che per loro è molto viscoso, come una
specie di melassa. Assumendo per le ali del calabrone un valore così basso e una
superficie liscia, si doveva supporre che il flusso dell’aria su di esse fosse laminare, ossia
privo di turbolenze. Questo comportava una mancanza di adesione tra l’aria e la superficie dell’ala con conseguente perdita di portanza, la grandezza che sostiene un
aereo in volo e ne impedisce lo "stallo", ossia la caduta verticale. Intuitivamente
l’aerodinamica del calabrone non è delle migliori: mentre gli uccelli hanno un’apertura alare che permette loro di planare per lunghi tratti, le ali di questi insetti sono ridicolmente piccole e se
raccogliamo un calabrone morto e lo lasciamo cadere, questo precipita a terra come una pietra per effetto del proprio peso. Come
risolvere allora il mistero del suo volo? La risposta è che l’insetto ha trovato un modo per sostenersi nell’aria, sfruttando la turbolenza
creata dal furioso sbattere delle sue piccole ali. Già nel 1975, Christopher Rees comunicava sulla rivista scientifica Nature alcune
osservazioni sulla forma e la funzione della corrugazione nelle ali degli insetti, osservando che la
successione di sezioni fortemente irregolari che le caratterizzavano avevano dei grossi vantaggi aerodinamici senza compromettere l’aerodinamica. In effetti, lo
scienziato mostrava come, mettendo in un grafico la portanza e la resistenza aerodinamica di
queste ali, esse mostravano caratteristiche simili a quelle del profilo alare convenzionale
di un aeroplano. Ma le spiegazioni più recenti sul volo degli insetti hanno
imboccato un percorso diverso da quello dell’aerodinamica classica, prendendo in considerazione gli accorgimenti per volare in
condizioni di instabilità. Ritornando al nostro calabrone, era necessario spiegare come riuscisse a sfruttare la turbolenza
aerodinamica che creava attorno a sé per mantenersi in volo. Ormai era chiaro che l’aerodinamica degli insetti era diversa da quella
fino ad allora studiata dai tecnici aeronautici, che consideravano delle
ali fisse e un flusso d’aria uniforme. Utilizzando riprese cinematografiche ad alta velocità dei battiti delle ali, e confrontandole con modelli di simulazione al computer, si scoprì
attorno al 1990 che gli insetti creavano dei vortici d’aria attorno a un nucleo centrale2. In questo modo la portanza, ossia la forza che li tiene
in volo, non era generata in modo continuo, come avviene per le ali degli aerei, ma a scatti. In effetti, gli insetti usano le loro ali in
modo più simile a quello degli elicotteri che a quello degli aeroplani per spostarsi orizzontalmente, ma anche verticalmente, in
diagonale e per restare sospesi nell’aria. A differenza degli elicotteri, che hanno un asse centrale di rotazione, questi animaletti
battono le ali verso il basso, quindi le ruotano verso l’alto, le ribattono verso l’altro, le
ruotano di nuovo e così via; questi movimenti non avvengono necessariamente verticalmente rispetto al suolo ma anche obliquamente, permettendo di manovrare nello
spazio. I vortici creati da queste manovre fanno scorrere più velocemente l’aria nella
superficie superiore dell’ala che in quella inferiore, creando una differenza di pressione che genera la portanza necessaria per mantenersi in volo. Il pericolo in agguato, a
questo punto, diventa lo stallo, ossia la perdita improvvisa di portanza che dipende
dall’angolo tra l’ala e il flusso d’aria che arriva su di essa.
Quando un’ala con un grande angolo d’attacco è accelerata fortemente, si crea temporaneamente un nuovo vortice
d’aria che aggiunge portanza ritardando lo stallo. Per gli insetti si riteneva che questo fenomeno fosse troppo effimero per contribuire
significativamente alle loro capacità di volo, ma nel 1996 Charles Ellington e un gruppo di collaboratori del Dipartimento di Zoologia
dell’Università di Cambridge in Inghilterra, dimostrarono il contrario3. I ricercatori studiarono la Manduca Sexta, una falena che era
già stata utile alla scienza negli studi di endocrinologia e di neurologia. Ellington e soci utilizzarono le osservazioni effettuate con una
tecnica fotografica tridimensionale dei movimenti delle ali e un’analisi al computer delle stesse. Confrontarono quindi il tutto con il
comportamento di the flapper: un robot che imitava meccanicamente i movimenti e le deformazioni delle ali dell’insetto con una
frequenza di battito inferiore per tener conto delle dimensioni dieci volte superiori a
quelle della Manduca. I ricercatori scoprirono che in questa situazione si formava sul bordo delle ali un vortice che restava attaccato alle stesse, muovendosi a spirale lungo la
superficie e creando una zona di bassa pressione. Questo spiegava perché gli insetti sapevano creare una portanza tre volte
superiore a quella che risulterebbe dai calcoli dell’aerodinamica convenzionale e perché non avveniva lo stallo che ci si sarebbe
aspettato in quelle condizioni. Le osservazioni fotografiche delle turbolenze che si
formavano lungo le ali di the flapper, quando questo era messo in una "camera a fumo", mostrarono chiaramente il fenomeno nel suo verificarsi. In seguito a questo lavoro
pionieristico, in vari laboratori sono stati messi a punto differenti modelli meccanici per
comprendere sempre più accuratamente il volo degli insetti anche se gli studi dovranno protrarsi ancora per anni prima di poter sperare di vedere un robot-insetto in grado di
volare autonomamente4.
La formazione del "vortice spiraliforme" era una buona spiegazione nel caso di grossi insetti con
un’apertura alare relativamente ampia. Nel caso degli insetti più piccoli, però, le forze di viscosità tendevano a dissipare molto presto
il vortice ed era necessario trovare un ulteriore meccanismo che permettesse loro di volare5. Ancora una volta la soluzione venne
da un insetto-robot che simulava la Drosophila: un altro animale studiatissimo dalla ricerca genetica e biologica. Nel 1999 comparve
sulla rivista Science un articolo firmato da Michael Dickinson, un esperto di fisiologia e di meccanica del volo e un gruppo di
collaboratori6: gli scienziati avevano immerso in olio minerale un modello meccanico di Drosophila di 24 centimetri per simulare la
viscosità che l’insetto reale prova mentre volava; una serie di motori collegati alle ali del robot permetteva la simulazione dei
movimenti reali inclusa la rotazione al termine di ogni battito. Attraverso una serie di trasduttori di pressione collegati alle ali, gli
studiosi misurarono delle forze superiori a quelle che ci si sarebbe aspetti in condizioni non
dinamiche. Succedeva che con il movimento delle ali l’insetto "catturava" il vortice
formato durante il precedente battito. Un altro fattore cruciale evidenziato dai
ricercatori era l’elevata sensibilità a piccole alterazioni nella sincronizzazione della
rotazione delle ali, in grado di cambiare in modo considerevole sia l’intensità sia la direzione delle forze che agivano su di esse: nella "aerodinamica instabile" del mondo
degli insetti anche questo era da mettere in conto.Le più recenti teorie e i modelli proposti sul volo degli insetti sono in grado di spiegare il
paradosso del volo del calabrone? Gli esperti sono propensi a credere che ogni tipo di insetto abbia sviluppato il
suo modo particolare di sfruttare l’aerodinamica instabile. L’osservazione diretta e il confronto con simulazioni al computer e modelli meccanici
hanno svelato i segreti del volo di alcuni insetti come la Drosophila e la Manduca; non ci sono ragioni per credere che ciò possa
avvenire anche per il nostro calabrone. Frattanto, in questi ultimi anni, i progressi nella comprensione dell’aerodinamica degli insetti
sono stati costanti al punto che gli specialisti credono che la creazione dei primi insetti robotizzati sia ormai a portata di mano7.
Ribattezzati Microveicoli aerei (MAV) essi saranno dotati di minuscoli
trasmettitori radio ed altri sensori, e potranno essere impiegati per volare in luoghi angusti e difficoltosi da raggiungere per gli uomini; ad esempio, controlleranno la tenuta e il livello di sicurezza
della complessa rete di tubazioni che trasportano i gas e le sostanze chimiche nelle grosse industrie. Attualmente, almeno tre
nazioni stanno studiando i propri MAV e, ovviamente, non è mancato l’interesse per possibili impieghi
militari e nel campo dello spionaggio; se questi saranno portati a termine, il povero
calabrone e coloro che ne hanno studiato l’impossibile volo, sono
innocenti.
|
|
IL MANTICE DELLA FORZA SERPENTINA DI SETH
|
|
Ed ora proseguiamo la ricerca su Seth, stimando interessante il lato geometrico che vi potrebbe
corrispondere. La ruota a palette spiraliformi, disegnata sotto l'ascella di Seth, ci porta alle spire del «cobra»
(illustr.20), riportata di seguito, onnipresenti nell'iconografia degli antichi egizi. E quì abbiamo il modo di
agganciarci alla geometria cheopiana trattata nel mio saggio più volte menzionato, «Alle radici
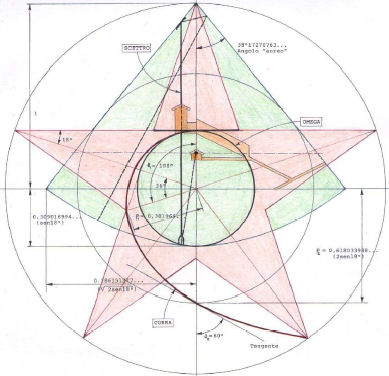
dell'intelligenza matematica». Basta l'illustr.19 della configurazione della pentastella, che segue, per
accettarne i rilievi per poi traslarne il concetto al mio supposto «pensare geometrico degli antichi egizi»8.
Attraverso la pentastella e l'ideogramma egizio che vi corrisponderebbe (una pentastella, appunto, in due
versioni: sormontata da una luna crescente parziale e totale) si scoprono delle relazioni illuminanti, sia con la
ruota a palette spiraliformi sotto l'ascella di Seth, che con l'analoga dell'uomo che vi corrisponde, la spalla.
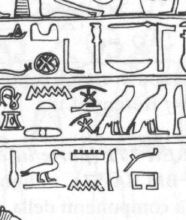
Per quanto concerne le due versioni della pentastella, attraverso l'illustr.21 si vede il disegno della sommità
della stele BM 571 di calcare (conservata nel Britisch Museum di Londra) in cui compare al centro
l'ideogramma della stella in questione, sormontata da una luna crescente e che si vede meglio dal dettaglio
relativo ingrandito dell'illustr.22. Le spiegazioni del dettaglio a riguardo si rilevano dall'illustr. 23.
|
|
|
|
Illustrazione 19 - Configurazione della stella a cinque punte e la relativa geometria del “cobra” in relazione della piarmide di Cheope. (vedasi saggio dell'autore “Alle radici dell'intelligenza matematica”) |
|
|
|
 |
|
 |
|
Illustrazione 22 -
Dettaglio della sommità della stele Bm EA 571. Al centro si nota
l'ideogramma della pentastella sormontata dalla luna crescente |
|
Illustrazione 20 - Il "cobra". Dettaglio dell'affresco della cappella funeraria di Tuthmosi III |
|
|
|
 |
|
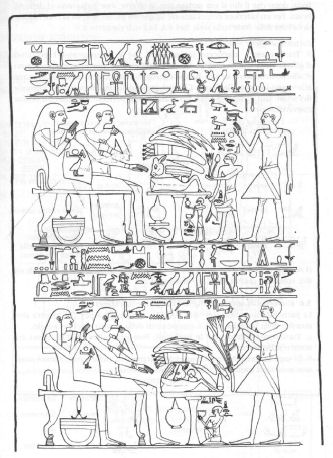
Illustrazione 21 - Sommità della stele egizia in calcare, BM EA 571 conservata nel
Brutisch Museum di Londra |
|
|
|
 |
|
Illustrazione 23 - Sulle stele sono spesso rappresentate alcune feste particolari o periodiche in cui compaiono questi ideogrammi. Qui si tratta della stele in calcare Bm EA 571 (sommità)
conservata nel Britisch Museum di Londra (vedi illustr.21 e 22) |
|
|
|
|
LA CUFFIA DEI ROTATORI DELLA SPALLA UMANA
|
|
Non meraviglia immaginare che i diversi movimenti cui attende la funzione delle braccia, vere e proprie leve di
forza fulcrate nella spalla, servano per muovere ben altro che non sappiamo. Per esempio ad azionare una
sorta di mantice, da riferirsi alla misteriosa ruota a palette spiraliforme dell'ascella di Seth. Questa ipotesi
porterebbe a trovare la relazione con la forza serpentina del «cobra» che fa capo alla meravigliosa geometria
cheopiana quale mirabile radice del pensiero umano. Ecco dunque ciò che prima non si
vedeva ed ora sì: un cielo nella pentastella e una terra lunare (il perispirito degli ermetisti
cui si riferisce Giuliano Kremmerz, quando descrive il mondo
astrale) per «la festa mensile» a portata di mano, secondo l'interpretazione
dell'ideogramma in discussione di Mark Collier e Bill Manley che hanno scritto il testo «Come leggere i
geroglifici egizi», ediz. Giunti, da cui ho tratto alcuni frammenti qui riportati. Ora resta della spalla
perfezionare la sua anatomia per intravederne la cuffia rivelatrice di relazioni sul filo dell'incertezza.
|
|
LA SPALLA IN BREVE
|
|
www.spalla.it/spalla.html
|
|
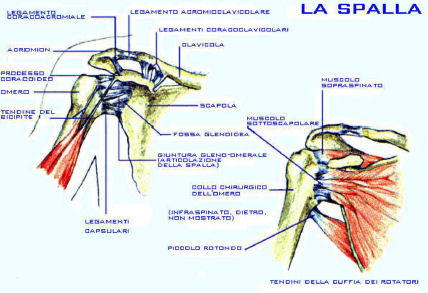 La spalla è un complesso sistema costituito da tre ossa (scapola - omero - clavicola)
che sono in rapporto tra di loro mediante muscoli, tendini e legamenti. La spalla è un complesso sistema costituito da tre ossa (scapola - omero - clavicola)
che sono in rapporto tra di loro mediante muscoli, tendini e legamenti.
La clavicola unisce la spalla alla gabbia toracica, tenendola lontana dal tronco, e collegata per mezzo dell'articolazione
acromion-claveare alla scapola, che è larga, piatta e triangolare.
L'acromion si protende dalla scapola per formare una sorta di copertura.
Dal processo coracoideo – anch'esso parte della scapola – origina il capo breve del
bicipite. La testa dell'omero e la cavità glenoidea con i legamenti gleno omerali
costituiscono l'articolzione gleno omerale che è la più mobile del corpo. In definitiva
la spalla è l'espressione dei movimenti coordinati di più articolazioni: la gleno-omerale, la scapolo-toracica,
l'acromionclaveare e la pseudo articolazione sub-acromiale.
Tra l'acromion e la cuffia è presente una borsa "ammortizzatore" che svolge una funzione di cuscinetto tra i tendini e l'osso
sovrastante. Questa piccola sacca può facilmente infiammarsi.
La cuffia dei rotatori è l'insieme dei tendini (sottoscapolare, sovraspinato, sottospinato e piccolo rotondo) che avvolgono la testa
omerale, hanno funzione di centramento e stabilizzazione della gleno-omerale. Sono rotatori e abduttori.
Ogni volta che si solleva il braccio la cuffia dei rotatori e la borsa vengono compressi.
|
|
CORRELAZIONI CON LA
MAGIA
|
|
Sembra che ora tutta l'attenzione sia incanalata verso l'emblematico dio del male, Seth, come una sorta di
«fantasma dell'opera» che ha che fare con un personaggio del papiro di Ani, il dio Toth dalla testa d'ibis,
patrono della magia neutrale, e non malvagia che è quella di Seth. Infatti nel papiro di Ani, quello della
pesatura del cuore, Seth appare come un cane accucciato tenuto a bada da Toht tutto indaffarato a scrivere il
verdetto del giudizio sul cuore di Ani col calamo. Ora occorre riassumere un paio di elementi che sono emersi sul conto di Seth e che fanno capo ad una sua
forza virulenta, la «forza serpentina», quella del «cobra», aderendo alla diffusa iconografia dell'antico Egitto
che lo raffigura. Il primo elemento è il mantice della forza serpentina che permette a Seth di
“volare” contro tutte le regole “fisiche” (trasalte alla relativa sua dimensione
esistenziale), e le ipotesi scientifiche sul calabrone e insetti simili lo dimostrerebbe. Ed è in questa condizione di supremazia che Seth si dimostra
come un dio. Il secondo elemento è l'origine dell'energia necessaria per far sostentare nella
“melassa” infera il dio Seth, e sembra derivare dal movimento delle braccia umane nel punto preciso della «cuffia dei rotatori».
Da qui anche una interessante simbologia egizia della luna a cavalcioni della pentastella (questa stella è
sinonimo di “adorare” in stretta relazione col “sacerdozio”). Nulla ci vieta, avendo toccato il tasto della magia,
di andare a curiosare fra le carte di un noto maestro di magia, Aleister Crowley (1875-1947), e precisamente
nel suo libro «Magick» edito dalla Casa Editrice Astrolabio.
Comincio dalla configurazione dei «segni dei gradi inziatici» che sono 10 rappresentati nell'illustr.25.
Si notino le figure 1 e 9 dell'illustr.25. La 1 è il segno di «Terra» e rappresenta il dio Set (o Seth) che
combatte con il braccio destro alzato. La 9 è il segno V di Tifone – il
Tridente, e qui sono alzate entrambe le braccia. E' presumibile che le braccia alzate
abbiano a che vedere con potere serpentino generato proprio sotto l'ascella delle braccia. Poi c'è
dell'altro che convaliderebbe la natura specifica del potere serpentino in discussione.
A pag. 259 del libro Magick si parla dei gesti ed in particolare del movimento principale nel Cerchio, la
«circumambulazione». Però il movimento che più interessa per noi, è a spirale. Riporto ora le parole
precise del libro in proposito: «Un altro movimento importante è la spirale, di cui esistono due
forme principali: una dall'esterno all'interno, l'altra dall'interno all'esterno. Possono venire eseguite in entrambe le direzioni:
compiute in senso orario, servono per invocare, in senso antiorario servono per bandire9.
Nell'esecuzione della spirale, il passo è, lieve e agile, quasi simile ad una danza: mentre la
esegue, il mago di solito gira su se stesso, ...». Per chiudere il capitolo su Magick schiarisce l'argomento sul misterioso Seth la nota 25 a pag.455 di seguito
riportata:
«L’intero rituale è un’invocazione di Shaitan (Satana) o Set, il figlio di Osiride. Crowley si serve di altri temi magici e li rimodella alla
luce del suo scopo in questa particolare operazione, che è l’unione con il suo Angelo, Shaitan-Aiwass. A questo scopo il Papa (o
Gerofante o Grande Sacerdote) dei Tarocchi, il cui numero è V, viene sostituito dal
Diavolo, Set, il cui numero nei Tarocchi è XV. Perciò, invece di “Cinque per funzione”, si
legge “Quindici per funzione”. Cioè Horus (o Set) ha ormai sostituito Osiride (il Papa) nel
Nuovo Eone. Analogamente l’Arcano dei Tarocchi detto l’Eremita, attribuito alla Vergine,
è “Nove per natura”. E' rappresentato dalla Yod o I della formula IAO. L’A di questa formula è “Il Matto”, la cui lettera è
Aleph, che è lo O nei Tarocchi: “Zero per conseguimento”. La O della formula è il Papa o Gerofante, non come Osiride (V), bensì come Set, il Diavolo, la cui lettera è O».
|
|

|
| Illustrazione 25 – Dal libro «Magick »
di Aleister Crowley. I segni dei gradi iniziatici |
|
|
|
|
CORRELAZIONI CON LA
BIBBIA
|
|
Al gesto delle braccia alzate per esorcizzare la temibile forza serpentina, testè rilevata ricorrendo al libro
«Magick» di Aleister Crowley, non sembra estraneo Mosè biblico. Di lui sappiamo che era stato iniziato alla
magia degli egizi, prima di porsi a capo del popolo ebraio per liberalo dallo stato di schiavitù in Egitto. Il potere
magico del «cobra» era ben noto a Mosè e lo dimostra leggendo il seguente passo dell'Esodo 17,8-13:
«In quei giorni, Amalek venne a combattere contro Israele a Refidim. Mosè disse a Giosuè: «Scegli
per noi alcuni uomini ed esci in battaglia contro Amalek. Domani io starò ritto sulla cima del colle con
in mano il bastone di Dio». Giosuè eseguì quanto gli aveva ordinato Mosè per combattere contro
Amalek, mentre Mosè, Aronne, e Cur salirono sulla cima del colle. Quando Mosè alzava le mani,
Israele era il più forte, ma quando le lasciava cadere, era più forte Amalek. Poiché Mosè sentiva
pesare le mani dalla stanchezza, presero una pietra, la collocarono sotto di lui ed egli vi sedette,
mentre Aronne e Cur, uno da una parte e l’altro dall’altra, sostenevano le sue mani. Così le sue
mani rimasero ferme fino al tramonto del sole. Giosuè sconfisse Amalek e il suo popolo.»
|
|
LA FINE DEL REGNO DEI MILLE ANNI?
|
|
E per concludere il saggio, immaginando il dio Seth quasi rabbonito, quindi a piede libero, viene da pensare
al passo 20 dell'Apocalisse di Giovanni apostolo che predice il regno dei mille anni ed il seguito fino alla prima
resurrezione, quella dei beati e santi.
Riporto la prima parte del passo in questione:
«Vidi poi un angelo che scendeva dal cielo con la chiave dell'Abisso e una gran catena in mano.
Afferrò il dragone, il serpente antico - cioè il diavolo, satana - e lo incatenò per mille anni; Lo gettò
nell'Abisso, e ve lo rinchiuse e ne sigillò la porta sopra di lui, perchè non seducesse più le nazioni,
fino al compimento dei mille anni. Dopo questi dovrà essere sciolto per un po' di tempo. Poi...»
Sorge ora una perplessità non da poco: visto che fa capolino l'Apocalisse di
G., il tema di questo saggio, "Sul terzo giorno giorno", non riporta una parola
in più che vi attiene e che qui manca? Infatti l'apostolo Giovanni (che profetizza gli eventi relativi ai «due
Testimoni, vestiti di sacco») dice chiaramente
«...ma dopo tre giorni e
mezzo,...» (Ap. 11,11).
Manca un altro «mezzo» giorno allora? Come per dire che i fatti di Dio,
secondo il Cristianesimo, contemplano un genere di orologio diverso. No di
certo. Allora questo significa che, interpretando la cosa in modo ermetico cui
anche Giovanni deve avervi fatto ricorso, «mezzo» vuole indicare mediazione.
Semplice, no? Sì ma...». Ma occorre entrare nei dettagli per capire chi sono i «due Testimoni vestiti di sacco», sempre dell'Apocalisse
giovannea, che «dopo tre giorni e mezzo» resuscitarono con «un soffio di vita procedente da Dio» «con
grande terrore di quelli che stavano a guardarli»!
|
|
|
|
NOTE
|
|
1) John McMasters, "The flight of the bumblebee and related myths of entomological engineering", American Scientist, vol. 77, 1989, pp. 164-169.
2) Robin Wootton, "How flies fly", Nature, vol. 400, 8 luglio 1999, pp. 112-113.
3) Charles P. Ellington et all, "Leading-edge vortices in insect flight", Nature, vol. 384, 19/26 dicembre 1996, pp. 626-630.
4) Gary Taubes, "Biologists and engineers create a new generation of robots that imitate life", Science, vol. 288, 7 aprile 2000, pp. 80-83.
5) Robert Dudley, "Unsteady aerodynamics", Science, vol. 284, 18 giugno 1999, pp. 1937-1939.
6) Dickinson M. H., F. O. Lehmann, et al., "Wing rotation and the aerodynamic basis of insect flight", Science, vol. 284, 18 giugno 1999, pp. 1954-
1960.
7) Robin Wootton, "From insects to microvehicles", Nature, vol. 403, 13 gennaio 2000, pp. 144-145.
8) – Vedasi:
scienzaespirito.etanali.it oppure
specchiomagico.net/gbarbella.htm
9) - «...Certe forze formidabili possono essere invocate con la circumambulazione. In senso antiorario quando è eseguita con intenzioni contrarie a esse a alla tecnica iniziatica. Di tali forze Tifone è il tipo e la guerra dei Titani contro gli Dei Olimpici la leggenda . (Teitan, Titano, ha in greco il valore numerico di 666).
|
|
|
|
|
|
|
|
|
|
